Insertion Sort - Algorithm (Simple sorting Techniques)

Hi, I described two simple sorting techniques in previous two posts. This post will describe Insertion sort.
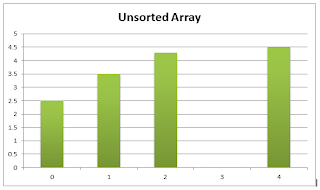
Look at the following Unsorted array.

figure 01

Takeout an element  from the array. Compare it with the elements with lower indexes. Shift those elements to right while find a smaller element than element 1. If n'th element is smaller than the selected element , insert element 1 in n+1'th place. 

Round 01:

Step 01: Takeout element 1 from the array(figure 02).

figure 02

Step 02: Compare element 1 with element 0. element 0 is larger than element 1. So shift element 0 to position 1(figure 03).

figure 03

Step 03: Insert element 1 in position 0(figure 04).

figure 04

Round 02:

Step 01: Takeout element 2 from the array(figure 05). Assign it to a temp variable.

figure 05

Step 02: Compare temp with element 1. element 1 is larger than temp. So shift element 1 to position 2   (figure 06)

figure 06

Step 03: Compare temp with element 0. element 0 is smaller than temp. So insert temp in position 1     (figure 07).

figure 07

Round 03:

Step 01: Takeout element 3 from the array(figure 08) and assign it to temp. 

figure 08

Step 02: compare temp with element 2. element 2 is larger than temp. So no need to shift. temp inserted in the position 3(figure 07).

Round 04:

Step 01: Takeout element 4 from the array(figure 09) and assign it to temp.

figure 09

Step 02: Compare temp with element 3. element 3 is larger than temp. So shift element 3 to position 4  (figure 10). 

figure 10

Step 03: Compare temp with element 2. element 2 is larger than temp. So shift element 2 to position 3  (figure 11).

figure 11

Step 04: Compare temp with element 1. element 1 is larger than temp. So shift element 1 to position 2  (figure 12).

figure 12

Step 05: Compare temp with element 0. element 0 is smaller than temp. So no need to shift. Insert temp in position 1(figure 13)

figure 13

Overview

After four Rounds, the array is sorted.This technique can used  when a part of the array is already sorted. This technique is better for almost sorted arrays.  

figure 14: a partially sorted array 

We don't need to worry about the sorted area. We can start the sorting from the beginning of the unsorted area. According to figure 14, sorting should start with element 5.

  Java code for Insertion Sort

 The Runner class

Download the code from here 

Selection Sort - Algorithm (Simple sorting Techniques)

Hi, This is the second part of Simple sorting techniques. I described Bubble sort   in previous post. So this post describes the Selection Sort.
consider the following unsorted array.

figure 01: unsorted array 

Round 01:(Consider all five elements)

Step 01: Mark the 0th element as minimum of the array. Then compare the current minimum with other elements. If one of the other elements is smaller than current minimum, that element become the current minimum.

figure 02: current minimum is element 0

Compare current minimum with element 1. Element 1 is smaller than current minimum. So element 1 become the current minimum. 

figure 03: current minimum is element 1

Then compare the current minimum with element 2, element 3 and element 4. But all of those elements are larger than element 2. Therefore at the end of Round 01, current minimum is element 1. 

Then current minimum should go to 0th position. And the element in 0th position come to the current minimum's position. So the current minimum and element 0 is swapped.

figure 04:current minimum go to 0th position 

At the end of Round 01, the 0th element is sorted. So it will not consider again. 

Round 02:(Consider four elements)

Step 01: Mark element 1 as current minimum (figure 05). 

figure 05

Step 02:  Compare current minimum with element 2. element 2 is smaller than current minimum. So element 2 marked as current minimum (figure 06).

figure 06

Step 03: Compare current minimum with element 3 and element 4. element 4 is smaller than current minimum. element 4 marked as current minimum (figure 07).

figure 07

At the end of Round 02, current minimum is element 4. It means element 4 is the minimum of next four elements of the array (element 1, element 2, element 3, element 4).

So the current element should come to position 1. So element 1 and element 4 swapped. 

figure 08: current minimum goes to position 1

At the end of Round 02, the first two elements are sorted. So first two elements will not consider again. 

Round 03: (Consider three elements)

Step 01: Mark element 2 as the current minimum (figure 09).

figure 09

Step 02: Compare current minimum with element 3. element 3 is larger than current minimum. so element 2 remain as current minimum. Then compare current minimum with element 4. element 4 is larger than current minimum. So the minimum of next three elements(element 2, element 3, element 4) is in the right position. No need to swap. 

At the end of Round 03, first three elements of the array are sorted. So the first three elements will not consider again. 

Round 04:(last two elements considered)

Step 01: Mark element 3 as the current minimum (figure 10).

figure 10

Step 02: Compare current minimum with element 4. element 4 is smaller than current minimum. so element 4 become current minimum(figure 11).

figure 11

It means the minimum of last two elements of the array is element 4. so the current minimum should come to position 3. So element 3 and element 4 are swapped (figure 12).

figure 12

At the end of four Rounds, the array is sorted :)

Java code for Selection Sort

In selectionSort() method, the outer loop:

for (out = 0; out < nElemns-1; out++) reoresents the Rounds. For our example number of rounds are four. In each round out is increased by one.

min=out indicates the opening current minimum for the loop is out 'th element.

The inner loop :

for (in = out+1; in < nElemns ; in++) represents the steps. As our example in the first round, out is 0. It means inner loop runs from 1(out +1) to 4(<nElemns).

While inner loop runs 1 to 4, if (values[in] < values[min])  min = in; runs for four comparisons. 

while this four comparisons running , if the condition satisfies in=n,  element n become current minimum. 

 The Runner class

Download the code from  Here

Bubble Sort - Algorithm (Simple sort techniques)

Hi, I'm going to describe you some simple sorting techniques. This post describes one of the simplest sorting algorithms. Bubble sort. It is done by  comparing and swapping the contiguous elements.
Look at the following unsorted array.

figure 01:Before sorting

1st Round (Consider all five elements)

Step 01:

     First we compare 0th and 1st elements of the array. You can see 0th element is 4.3 and it is larger than 1st element which is 2.5. So we swap 0th and 1st elements.

figure 02:After swapping 0th and 1st elements

Step 02:

In step01 we have done with first two elements. The next step is compare and swap(if necessary) 1st and 2nd elements. Now the 1st element is 4.3 and 2nd element is 3.5. The 1st element is larger than 2nd element.

So we swap 1st and 2nd elements.

figure 03:After swapping 1st and 2nd elements

Step 03:

Compare 2nd and 3rd elements. 2nd element is smaller than 3rd element. So it is not need to swap. 

figure 04:2nd and 3rd elements are not swapped 

Step 04:

Compare 3rd and 4th elements. 3rd is larger than 4th. So we swap.

figure 05:After swapping 3rd and 4th elements

After four steps the 4th element is sorted at the end of the 1st Round. So no need to consider 4th element anymore(4th element already sorted). Therefore we consider only the 0th, 1st, 2nd and 3rd elements in next round. 

2nd Round (consider first four elements)

Step 01:

Compare 0th and 1st elements. 0th is smaller than 1st. So no need to swap.

figure 06

Step 02:

Compare 1st and 2nd elements. 1st is smaller than 2nd. So no need to swap.

figure 07

Step 03:

Compare 2nd and 3rd elements. 2nd is larger than 3rd. So we swap 2nd and 3rd elements.

figure 08:After swapping 2nd and 3rd elements

Now the last two elements are sorted at the end of the 2nd Round. So we not consider 3rd and 4th elements In the next round (3rd and 4th elements already sorted).

3rd Round (Consider first three elements)

Step 01:

Compare 0th and 1st elements. 0th is smaller than 1st. So no need to swap.

figure 09

Step 02:

Compare 1st and 2nd elements. 1st is larger than 2nd. So we swap 1st and 2nd elements.

figure 10: After swapping 1st and 2nd elements

Now all the elements are sorted. :) 

The java code for Bubble Sort is follow 

In BubbleSort class, the most important method is bubbleSort() method. 

The outer for loop :

for(int out=nElemns-1;out>0;out--)  represents the Rounds I described in the algorithm. Executing this loop one time means executing one Round in the Algorithm.In each round it reduces the elements to consider by one. 

According to the five element array I described above, for the first time out is 4(that means we consider all five elements from 0 to 4). 

When the loop executing the second time out is 3(consider first four elements from 0 to 3).

The inner loop: for(in=0;in<out;in++)  represents the number of steps execute in each round. 

As our previous example, In the first Round, the out is 4. which means the number of steps in first Round is 4. Because we compare(always) and swap(when necessary)  4 contiguous pairs of elements in first round. 

When inner loop complete four steps, the outer loop reduce out by one (Because after first round, the last element is sorted and will not consider it again) Which means the number of steps of 2nd Round is 3. Because we compare and swap 3 contiguous pairs of elements in second round.(Because after the first round the 4th element is sorted and not consider in 2nd Round).

The runner class 

Download Code

    

Bracket Check program in Java

This post describes how to write a bracket check program in Java. Here also I use Stack class I used in previous post. The additional class is BracketCheck class.

Driver class should like this

public class Driv {

public static void main(String[] args) throws IOException {

// TODO Auto-generated method stub

BracketCheck brc=new BracketCheck("}hgy{gh[yssr)))");

}

}

So, the output should like this :)